Chapter 2 Spatial regression
Now that we have become somewhat familiar with the use of spatial information, we will incorporate them into our linear regression code. The objective is to retrieve the information necessary to calibrate (and validate) the regression model from the original GIS layers and produce a spatialized prediction. Note that the data from regression.txt was originaly retrieved from these GIS layers.
What we are going to do is to replicate the process of obtaining the information by incorporating some functions from the packages Maptools and raster. In order to carry out this process, we will use the layer weather_stations.shp and a series of raster layers in ASCII format (mde.txt, lat.txt, long.txt, d_medit.txt, d_atl.txt).
To some extent we will incorporate part of the code from Accesing spatial data into the linear regression model. Take into account that this is just an example and any regression model is a valid candidate for this procedure.
2.1 Building the dependent variable
We will start by getting the information about the dependent variable. The information we used in the previous version was a column named Tavg. Well, this piece of information is located within the attribute table of weather_stations.shp, specifically in the attribute called Tmed_MES. What we have to do now is loading the vector layer and get that column:
library(maptools)
wStation<-readOGR('Data/weather_stations.shp')## OGR data source with driver: ESRI Shapefile
## Source: "C:\Users\rmarc\Desktop\Copia_pen\European_Forestry_Master\module-3\Data\weather_stations.shp", layer: "weather_stations"
## with 95 features
## It has 10 fieldshead(wStation,n=5)## INDICATIVO AÃ.O MES NOMBRE ALTITUD
## 1 3013 2012 6 MOLINA DE ARAGON 1063
## 2 9307A 2012 6 SAN MARTIN DEL MONCAYO (D.G.A. 816
## 3 9311C 2012 6 BORJA (AYUNTAMIENTO) 440
## 4 9336L 2012 6 FUENDEJALON (D.G.A. 455
## 5 9337A 2012 6 PRADILLA DE EBRO 228
## T_MAX_abs T_MIN_abs TMed_MAX TMed_MIN Tmed_MES
## 1 32.8 3.2 23.8 8.4 16.10
## 2 33.0 6.5 22.8 10.7 16.75
## 3 36.5 9.0 26.8 14.6 20.70
## 4 35.0 11.0 26.7 14.7 20.70
## 5 35.0 10.0 27.9 15.1 21.50vdep<-wStation@data$Tmed_MES
vdep## [1] 16.10 16.75 20.70 20.70 21.50 17.80 18.35 16.35 16.50 18.70
## [11] 18.00 15.85 15.80 18.85 18.30 19.35 18.10 16.95 17.40 18.00
## [21] 19.55 20.85 19.85 18.80 21.90 21.95 16.80 22.15 22.15 19.85
## [31] 20.30 20.55 20.90 20.55 20.90 16.15 19.60 16.40 19.60 17.25
## [41] 17.00 19.00 20.65 22.30 22.05 20.60 17.90 21.75 17.45 18.45
## [51] 16.70 20.70 19.90 19.90 23.50 22.30 20.15 22.05 21.20 22.10
## [61] 21.75 21.00 21.60 21.75 20.70 20.05 20.00 20.20 21.00 19.80
## [71] 20.80 21.70 18.75 18.90 18.80 19.75 18.75 20.80 20.35 19.75
## [81] 19.70 22.15 20.80 23.35 19.15 22.95 21.30 21.65 22.75 23.20
## [91] 22.45 16.10 17.30 16.25 16.30Now we have the dependent variable stored in the object vdep.
2.2 Retrieving the independent variables
Creating the dependent variable is really easy. Obtaining the predictors is a bit much more difficult. The steps we are going to follow are:
- Get the coordinates of the weather stations from
wStation. - Load the raster layers in a
RasterStack. - Extract the values of the rasters in the stations location.
wStation.coords<-wStation@coords
names(wStation.coords)<-c('x','y')
library(raster)
list.rasters<-list.files('Data/variables_weather/',full.names = TRUE)
rasters<-stack(list.rasters)
vindep<-extract(rasters,wStation.coords)
colnames(vindep)<-c('d_atl','d_medit','lat','long','elevation')
head(vindep,n=5)## d_atl d_medit lat long elevation
## [1,] 271251 183121 4522150 593950 1100
## [2,] 162508 232762 4632550 600250 794
## [3,] 167966 213217 4632350 622050 432
## [4,] 176676 205230 4624850 627150 434
## [5,] 171488 195728 4635650 644150 211We brought a new function here which was already mentioned in Loading multiple raster layers but not yet described. I am talking about extract(). This function takes a raster or RasterStack and a set of location defined with a pair of coordinates to get the value of the pixels on the given locations. We use this function to build a table with our independent variables.
Now we have our dependent and independent variables. We just need to put them together in a table and proceed with the regression:
regression<-cbind(vdep,vindep)
colnames(regression)## [1] "vdep" "d_atl" "d_medit" "lat" "long"
## [6] "elevation"Remember we can merge vector and table objects with cbind(). As we can see, the recently created regression object is actually the combination of vdep and vindep. There are however a couple of minor issues. One is that the name of the dependent variable in regression which is named vdep. This is not a problem per se but we better give it a name that reflects best the information and that matches the one we saw in the linear regression example (Tavg). The other problem comes from the fact that the data argument in lm() and most regression algorithms require a data.frame object. We may have not noticed that the regression object is a matrix6. Before using regression in lm() we must transform it into a data.frame using data.frame():
regression<-data.frame(regression)
names(regression)[1]<-'Tavg'
names(regression)## [1] "Tavg" "d_atl" "d_medit" "lat" "long"
## [6] "elevation"class(regression)## [1] "data.frame"Now we are good to go and perform the regression as we did before
2.3 Spatial prediction
The main difference between what we did in the linear regression example and what we are going to do now comes from the prediction. Now we are ready to make a spatial prediction using our rasters object rather than apply predict() to a table object. First let’s fit the model7:
mod.lm<-lm(Tavg~long+lat+d_atl+d_medit+elevation, data=regression)
summary(mod.lm)##
## Call:
## lm(formula = Tavg ~ long + lat + d_atl + d_medit + elevation,
## data = regression)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.78337 -0.54167 0.02639 0.52917 1.53176
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -1.860e+02 8.473e+01 -2.195 0.0307 *
## long -4.534e-05 1.836e-05 -2.469 0.0155 *
## lat 5.120e-05 2.078e-05 2.464 0.0157 *
## d_atl 4.112e-05 1.562e-05 2.632 0.0100 *
## d_medit -3.497e-05 1.643e-05 -2.129 0.0361 *
## elevation -6.325e-03 4.685e-04 -13.501 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.7295 on 89 degrees of freedom
## Multiple R-squared: 0.8793, Adjusted R-squared: 0.8725
## F-statistic: 129.7 on 5 and 89 DF, p-value: < 2.2e-16Had we had a validation sample we’ll now proceed and calculate some perfomance indexes and keep improving and optimizing the model. Since I skipped that part I’ll focus on the new prediction approach, the so-called spatial prediction. It is no easy to distinguish between regular and spatial prediction because the name of the function we use is the same, predict(). But, they are not the same. The predict() we are going to use right now comes from the raster package whereas the other is in stats. Best way to tell them apart, well, the new predict has more arguments than the original. Furthermore the order of the required arguments is different:
names(rasters)<-names(regression)[2:6]
mod.pred<-predict(rasters, mod.lm,filename="tavg.tif",type="response",index=1, progress="window", overwrite=TRUE)## Loading required namespace: tcltkSee, the new predict() has more stuff to deal with:
- The order of the first 2 arguments (
modelanddata) are switched. - The
dataargument is now aRasterStack). - We can specify a file to save the prediction into a spatial raster layer (
filename=tavg.tif). - The remaining arguments are used to get a progress window and to ensure that we obtain a prediction in the same units that the dependent variable (
type="response"8)
And now we can plot the prediction as we do with any raster in R:
plot(mod.pred, ylab="Latitude", xlab="Longitud", main="Linear regression",col=heat.colors(15))
points(wStation,pch=21)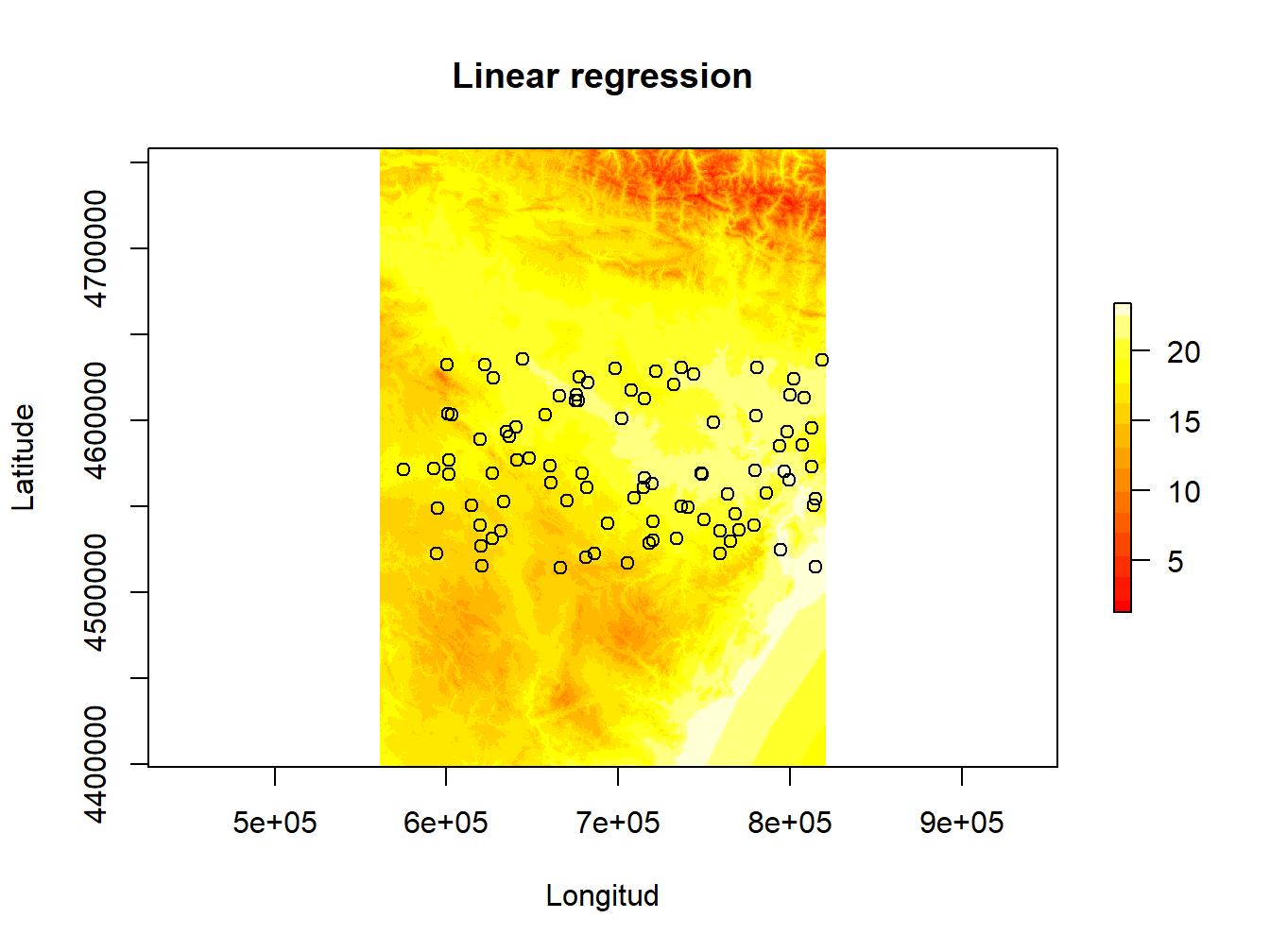
EXERCISE 7:
Modify the script for logistic regression of fire occurrence to adapt it to spatial regression model. Use the file fire_logit.csv to obtain the coordinates of the presence and absence points and the raster layers in the folder variables_fire.
In addition:
- Use a calibration sample with 75% of the data to fit the model.
- Use the remaining 25% as validation sample and calculate the RMSE.
- Create a spatial prediction of the model with lowest AIC.
Deliverables:
- Create a script (.R file ) with the instructions used.
- Document the script adding comments (#) describing each step of the procedure.
IMPORTANT: the prediction process may take a while or even crash depending on your computer power. If that is the case do not hesitate to contact me. For regression it should run fine but in the case of the logit regression and more complex models the computational demand scaltes quite a bit.
We have a hint in the use of
colnamesinstead ofnames. The first is formatrixorarraysand the later fordata.frames.↩I am skipping sampling into calibration and validation but you should not. I am also not doing the collinearity analysis but, again, you should.↩
This is particularly important in
glm(). Don’t forget it!!↩